Notes on Complex Analysis

Complex Numbers

• the building blocks of complex analysis
  • real part + imaginary part : $a + bi$
• operations with complex numbers: addition/subtraction, multiplication, division
• visualization: use argand diagram/complex plane
• complex numbers provide a more complete number system that allows for the solution of all polynomial equations

Analytic Functions:

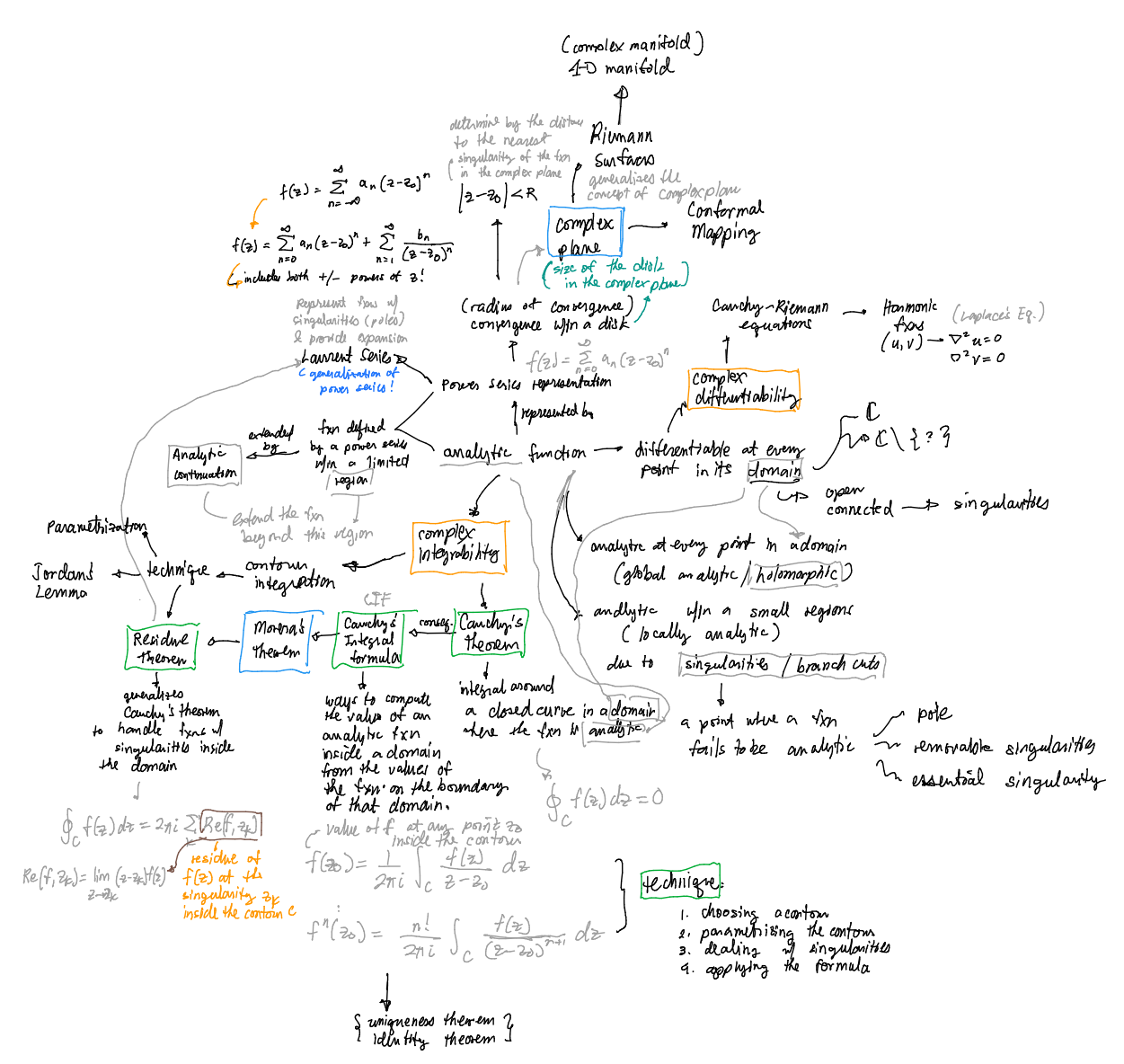
• Differentiable at every point in their domain (locally analytic within small regions, globally analytic/holomorphic if true in a domain).
• Represented by Power Series within a disk of convergence

• Satisfy Cauchy-Riemann equations, leading to Harmonic functions (Laplace Eq.).

• Complex Integrability:
  • Involves integrals around closed curves in a domain where the function is analytic.
  • Cauchy’s Theorem: Integral of an analytic function around a closed curve in a domain is zero.
  • Cauchy’s Integral Formula (CIF): Allows calculation of the value of an analytic function at any point inside a contour from its values on the boundary. It also provides formulas for derivatives.
  • Morera’s Theorem: Generalizes Cauchy’s theorem.

Singularities:

• Points where a function fails to be analytic. Types include removable singularities, poles, and essential singularities.
• Laurent Series can be used to represent functions with singularities (includes both positive and negative powers).
• Residue Theorem: Generalizes Cauchy’s theorem to handle singularities inside the domain. The integral is equal to 2πi times the sum of the residues at the singularities.

Mapping:

• Conformal Mapping: A complex mapping that preserves angles.
• Riemann Mapping Theorem: Relates to mapping a simply connected domain to the unit disk.

Other Concepts:

Complex Manifold: A 4-D manifold that generalizes the concept of a complex plane.

Jordan’s Lemma: Used in integration.

• Uniqueness Theorem/Identity Theorem: States that an analytic function is uniquely determined by its values on a set with an accumulation point.