Fundamentals of Physics

I found an old book [1] that discuss some ideas that is similar to what I have introduced in an old post about how to learn almost anything. The book introduces some of the fundamentals concepts of physics that are important to remember when studying different fields in physics because of its transferability and it may serve as an anchoring structure to make an order of the complexity of each field.

Fundamental physical concepts

I think these are the fundamental concepts that are not defined well in physics but assumed that readers know them by hindsight: physical system, states of the physical system, and the physical law. This dissection of physics is soo important, that it allows one to see the 3 operating objects in physics.

1. physical system : constitute a collection of physical object or even a single physical object
   • posses certain physical properties and can participate in various physical processess.
   • common way to characterize the properties of an objects and processes is to introduce various physical quantities.
2. state of a physical system : the objects in a physical system are interrelated both with each other and with external objects. This interrelationship manifests itself in the interactions of physical objects.
   • a change in position or state of a physical system will be called a physical phenomenon
   • physical phenomena are characterized by a change in a physical quantities which are interrelated
3. physical law is a necessary and stable interrelation or dependence between physical quantities. Constitute of 2 specific aspects:
   1. the conditions of its applicability : every physical law is valid only in certain conditions
   2. the method of application : every physical law has its method (algorithm) of application

The visualization of how physical laws are conceive are as follows:

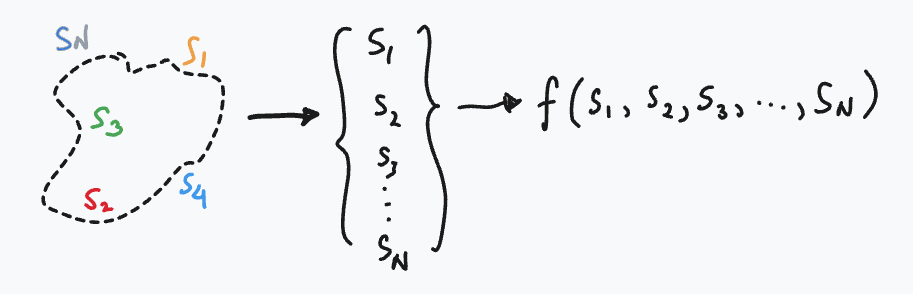
You choose a physical system you want to study (bounded) which can be describe by well selected important states $S_1, S_2, …, S_N$, which are related to each other according to some physical laws $f(S_1, S_2, …, S_N)$. One can think of physical laws as a function that relates the states into a certain way that provides the ability to interpolate and/or extrapolate other possible states.

The formulation and application of physical laws necessitate a sophisticated mathematical framework. This is where advanced techniques from differential equations, partial differential equations, special functions, Green’s functions, linear algebra, group theory, tensor calculus, and other mathematical methodologies become indispensable. These tools are not merely auxiliary; they are integral to both the rigorous derivation of physical laws and their practical deployment, transforming them from elegant theoretical constructs into powerful instruments for understanding and manipulating physical phenomena.

In Garrith’s book [2], he defines physics as “numbers in boxes”, which boils down to when different numbers represents the same physics - basically an equivalence problem. This numbers in the boxes are typically the properties that characterizes the physical objects (e.g. mass, charge, velocity).

In general physicist wants to find invariant laws, aka “conservation laws”.

I like this definitions because it coincides with my previous essay on how to learn almost anything. These concepts provides a simple anchoring system for the sometimes overwhelming discussions common in any physics books.

I tried to apply these concepts to some fields in physics:

1. classical mechanics
2. thermodynamis
3. electromagnetism
4. quantum mechanics
5. condensed matter physics
6. general relativity
7. quantum chemistry
8. particle physics
9. quantum field theory

Different Type of Physical Problems

The following key notes are from [1] part 3, which I think is useful for any beginning researcher in the field of physics: Formulated problems can be classified as: elementary, standard and non-standard. There are 3 stages in solving a formulated problem:

1. physical
2. mathematical
3. analysis of solution

Formulated physical problems can be categorized into three types: elementary, standard, and non-standard. Elementary problems require recalling and applying a single physical law and are sometimes referred to as training or plug-in problems. Standard problems, on the other hand, involve using a system of common knowledge and standard methods. Non-standard problems are the most original and challenging, requiring creative or advanced approaches to solve.

Solving these problems generally involves three stages: physical, mathematical, and analysis of the solution.

References

1. Belikov, B. S. (1989). General methods for solving physics problems. Mir Publishers.
2. Garrity, Thomas A. (2001). All the mathematics you missed: but need to know for graduate school.